Stock Market - Umme Salma M

The dataset used is stock market data of the Tata Consultancy Services (TCS) India over the last two decades (2000 – 2019). Here, we are exploring how to predict the VWAP (Volume Weighted Average Price). VWAP is a trading benchmark used by many traders. VWAP gives the average price the stock has traded at throughout the day, based on both volume and price. Many traders take positions based on the VWAP because of which it becomes very important to predict the value of VWAP.

Data Preparation

# Install the package using the following statement

!pip install pmdarima

# Import the required packages

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

import seaborn as sns

import missingno as msno

import plotly.express as px

import plotly.graph_objects as go

import matplotlib.dates as mdates

import scipy.stats

from sklearn.metrics import mean_absolute_error, mean_squared_error

import pylab

sns.set(style=’white’)

from pmdarima import auto_arima

from statsmodels.tsa.stattools import adfuller

import statsmodels.api as sm

from statsmodels.tsa.seasonal import seasonal_decompose

#Load the dataset

df=pd.read_csv(‘TCS.csv’)

#Converting Date into DateTime format

df[‘Date’]=pd.to_datetime(df[‘Date’])

df.set_index([‘Date’],inplace=True)

df.head()

# Displaying the summary of the data

df.describe()

df.shape

#Checking for the missing values

def missing_values_table(df):

# Total missing values

mis_val = df.isnull().sum()

# Percentage of missing values

mis_val_percent = 100 * df.isnull().sum() / len(df)

# Make a table with the results

mis_val_table = pd.concat([mis_val, mis_val_percent], axis=1)

# Rename the columns

mis_val_table_ren_columns = mis_val_table.rename(

columns = {0 : ‘Missing Values’, 1 : ‘% of Total Values’})

# Sort the table by percentage of missing descending

mis_val_table_ren_columns = mis_val_table_ren_columns[

mis_val_table_ren_columns.iloc[:,1] != 0].sort_values(

‘% of Total Values’, ascending=False).round(1)

# Print some summary information

print (“Your selected dataframe has ” + str(df.shape[1]) + ” columns.\n”

“There are ” + str(mis_val_table_ren_columns.shape[0]) +

” columns that have missing values.”)

# Return the dataframe with missing information

return mis_val_table_ren_columns

missing_table=missing_values_table(df)

missing_table

#Visualizing the locations of the missing data

msno.matrix(df)

# Removing missing columns which are also not an important feature.

df.drop([‘Trades’,’Deliverable Volume’,’%Deliverble’],axis=1,inplace=True)

#Exploratory Data Analysis

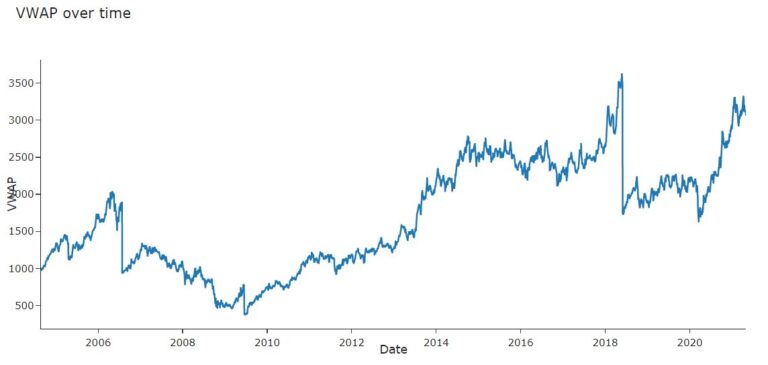
#Plot VWAP(Volume Weighted Average Price) over time.

fig = go.Figure([go.Scatter(x=df.index, y=df[‘VWAP’])])

fig.update_layout(

autosize=False,

width=1000,

height=500,

title=’VWAP over time’,

template=”simple_white”,

)

fig.update_xaxes(title=”Date”)

fig.update_yaxes(title=”VWAP”)

fig.show()

#VWAP 2019

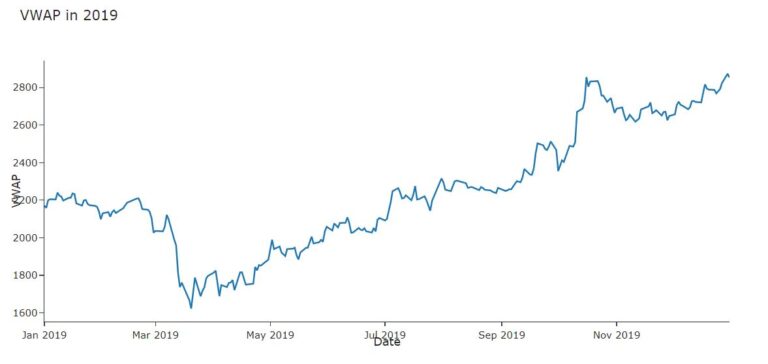
fig = go.Figure([go.Scatter(x=df.loc[‘2019’, ‘VWAP’].index,y=df.loc[‘2020’, ‘VWAP’])])

fig.update_layout(

autosize=False,

width=1000,

height=500,

title=’VWAP in 2019′,

template=”simple_white”,

)

fig.update_xaxes(title=”Date”)

fig.update_yaxes(title=”VWAP”)

fig.show()

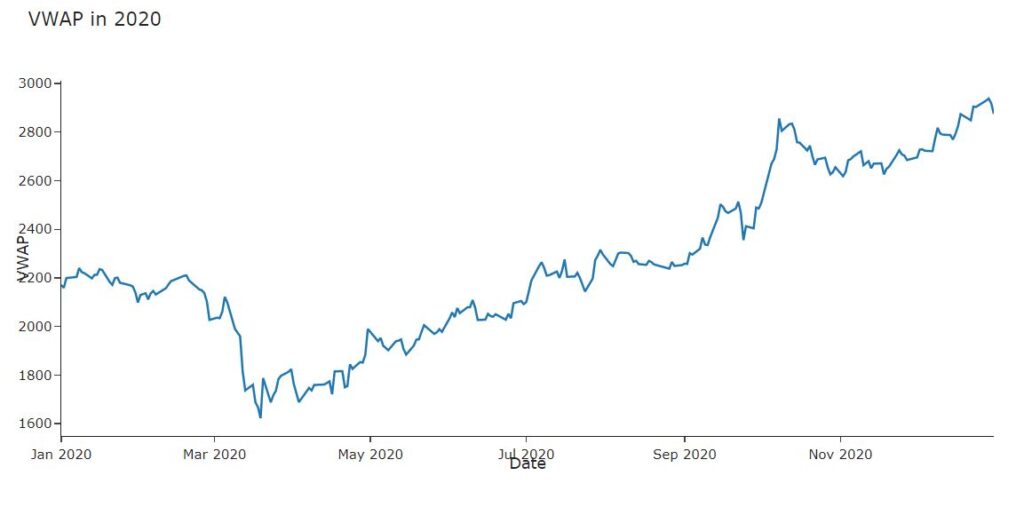
#VWAP 2020

fig = go.Figure([go.Scatter(x=df.loc[‘2020’, ‘VWAP’].index,y=df.loc[‘2020’, ‘VWAP’])])

fig.update_layout(

autosize=False,

width=1000,

height=500,

title=’VWAP in 2020′,

template=”simple_white”,

)

fig.update_xaxes(title=”Date”)

fig.update_yaxes(title=”VWAP”)

fig.show()

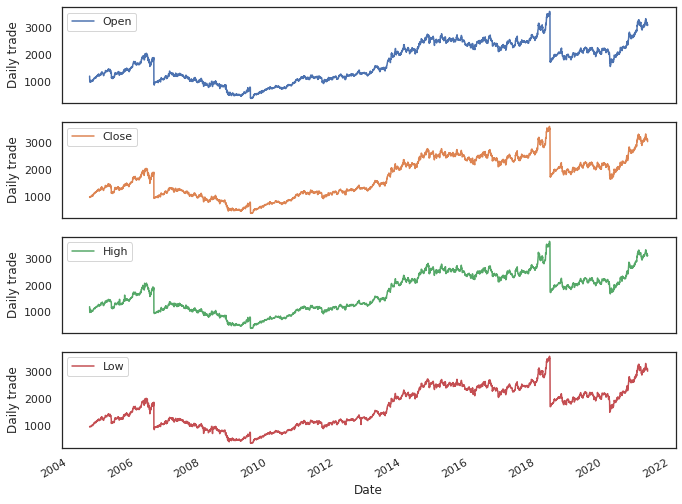
# Open, close,High, low prices over time

cols_plot = [‘Open’, ‘Close’, ‘High’,’Low’]

axes = df[cols_plot].plot(figsize=(11, 9), subplots=True)

for ax in axes:

ax.set_ylabel(‘Daily trade’)

#Open, close, High, low all are following the same pattern

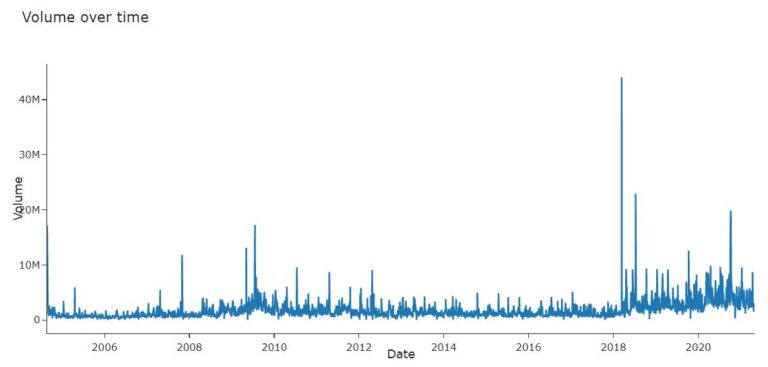
# Plot Volume over time

fig = go.Figure([go.Scatter(x=df.index, y=df[‘Volume’])])

fig.update_layout(

autosize=False,

width=1000,

height=500,

template=’simple_white’,

title=’Volume over time’

)

fig.update_xaxes(title=”Date”)

fig.update_yaxes(title=”Volume”)

fig.show()

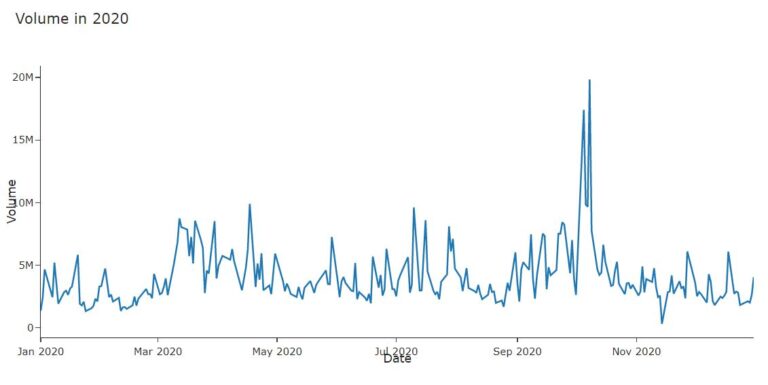
#Plot Volume in 2020

fig = go.Figure([go.Scatter(x=df.loc[‘2020’, ‘Volume’].index,y=df.loc[‘2020’, ‘Volume’])])

fig.update_layout(

autosize=False,

width=1000,

height=500,

template=’simple_white’,

title=’Volume in 2020′

)

fig.update_xaxes(title=”Date”)

fig.update_yaxes(title=”Volume”)

fig.show()

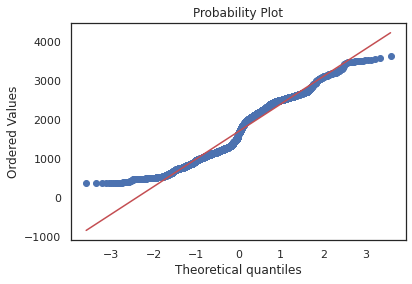
#Q-Q plot of VWAP is used to determine whether the dataset is distributed a certain way

scipy.stats.probplot(df.VWAP,plot=pylab)

pylab.show()

#Dicky Fuller Test

The Augmented Dickey-Fuller test is a type of statistical test called a unit root test.

The intuition behind a unit root test is that it determines how strongly a time series is defined by a trend It uses an autoregressive model and optimizes an information criterion across multiple different lag values.

The null hypothesis of the test is that the time series can be represented by a unit root, that it is not stationary (has some time-dependent structure). The alternate hypothesis (rejecting the null hypothesis) is that the time series is stationary.

Null Hypothesis (H0): If failed to be rejected, it suggests the time series has a unit root, meaning it is non-stationary. It has some time dependent structure.

Alternate Hypothesis (H1): The null hypothesis is rejected; it suggests the time series does not have a unit root, meaning it is stationary. It does not have time-dependent structure.

We interpret this result using the p-value from the test. A p-value below a threshold (such as 5% or 1%) suggests we reject the null hypothesis (stationary), otherwise a p-value above the threshold suggests we fail to reject the null hypothesis (non-stationary).

p-value > 0.05: Fail to reject the null hypothesis (H0), the data has a unit root and is non-stationary. p-value <= 0.05: Reject the null hypothesis (H0), the data does not have a unit root and is stationary.

def dicky_fuller_test(x):

result = adfuller(x)

print(‘ADF Statistic: %f’ % result[0])

print(‘p-value: %f’ % result[1])

print(‘Critical Values:’)

for key, value in result[4].items():

print(‘\t%s: %.3f’ % (key, value))

if result[1]>0.05:

print(“Fail to reject the null hypothesis (H0), the data is non-stationary”)

else:

print(“Reject the null hypothesis (H0), the data is stationary.”)

dicky_fuller_test(df[‘VWAP’])

#Seasonal Decompose

from statsmodels.tsa.seasonal import seasonal_decompose

from dateutil.parser import parse

plt.rcParams.update({‘figure.figsize’: (10,10)})

y = df[‘VWAP’].to_frame()

# Multiplicative Decomposition

result_mul = seasonal_decompose(y, model=’multiplicative’,period = 52)

# Additive Decomposition

result_add = seasonal_decompose(y, model=’additive’,period = 52)

# Plot

plt.rcParams.update({‘figure.figsize’: (10,10)})

result_mul.plot().suptitle(‘Multiplicative Decompose’, fontsize=22)

result_add.plot().suptitle(‘Additive Decompose’, fontsize=22)

plt.show()

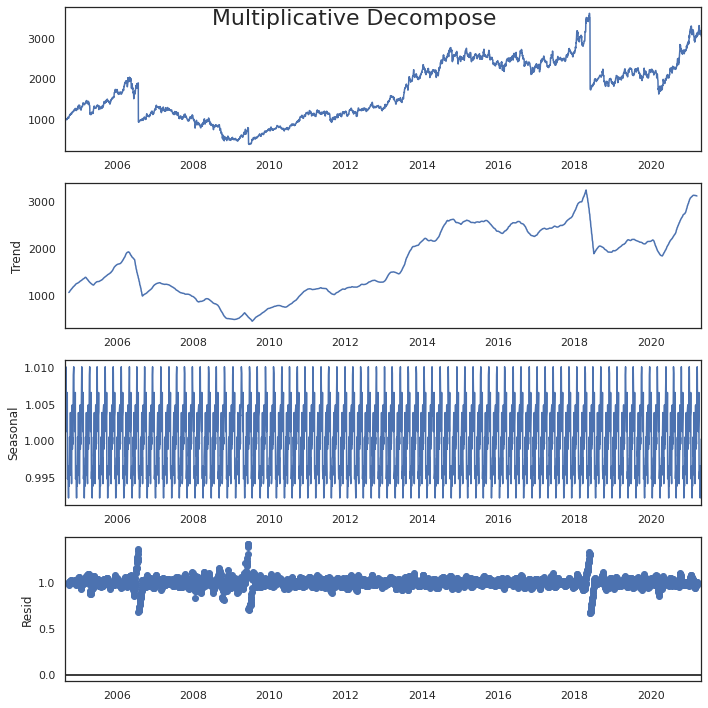
#Convert Stationary into Non-Stationary

# Differencing

df[‘vwap_diff’]=df[‘VWAP’]-df[‘VWAP’].shift(1)

fig = go.Figure([go.Scatter(x=df.index,y=df.VWAP)])

fig.update_layout(

autosize=False,

width=1000,

height=500,

template=’simple_white’,

title=’VWAP over time ‘)

fig.show()

fig = go.Figure([go.Scatter(x=df.index,y=df.vwap_diff)])

fig.update_layout(

autosize=False,

width=1000,

height=500,

template=’simple_white’,

title=’difference VWAP over time ‘)

fig.show()

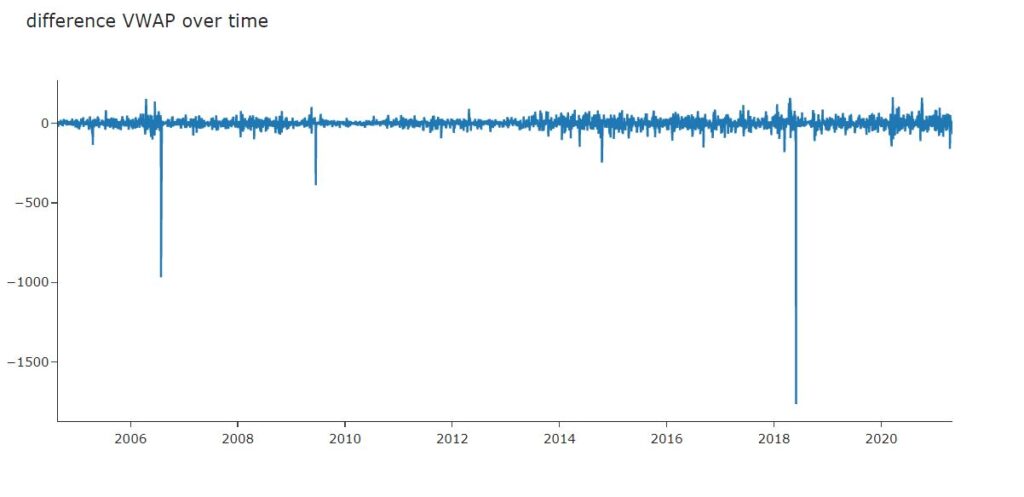
There is no need to convert the time series data into stationary data. This is done only for the purpose knowing how to check stationarity and how to convert non-stationary data into stationary data.

# Autocorrelation and partial autocorrelation plots

#Auto correlation of VWAP

sm.graphics.tsa.plot_acf(df[‘VWAP’].iloc[1:], lags=40,title=’auto correlation of VWAP’,zero=False)

plt.show()

#Auto correlation of difference VWAP

sm.graphics.tsa.plot_acf(df[‘vwap_diff’].iloc[7:], lags=40,title=’auto correlation of difference VWAP’,zero=False)

plt.show()

#Partial auto correlation of VWAP

sm.graphics.tsa.plot_pacf(df[‘VWAP’].iloc[1:], lags=40,title=’partial auto correlation of VWAP’,zero=False)

plt.show()

#Partial auto correlation of difference VWAP

sm.graphics.tsa.plot_pacf(df[‘vwap_diff’].iloc[1:], lags=40,title=’partial autocorrelation of difference VWAP ‘,zero=False)

plt.show()

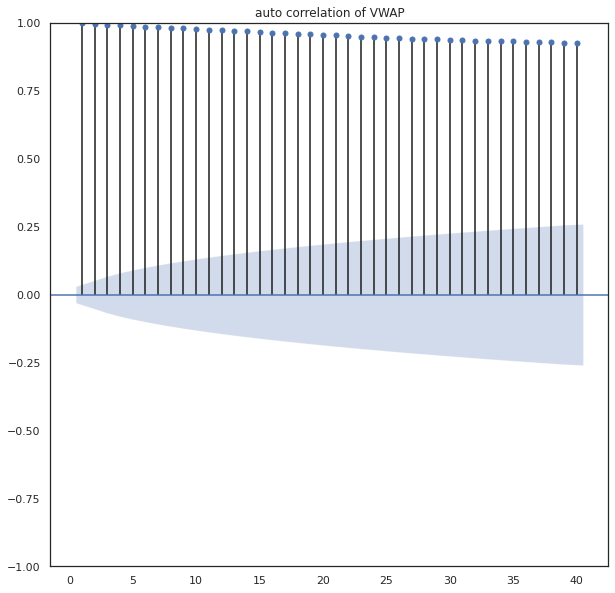
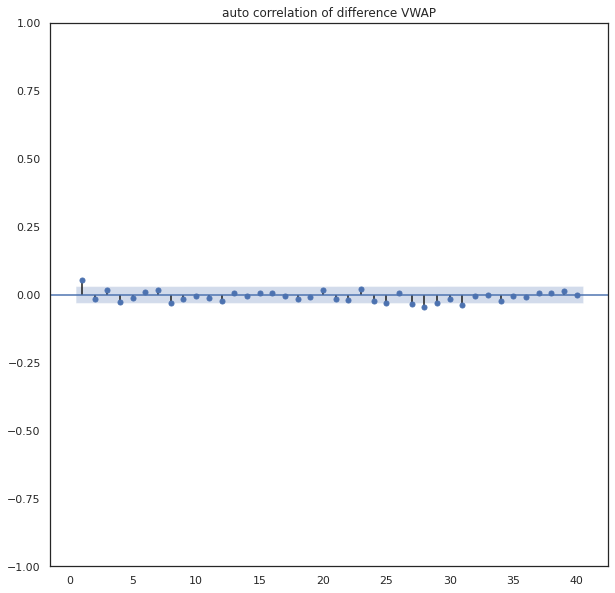
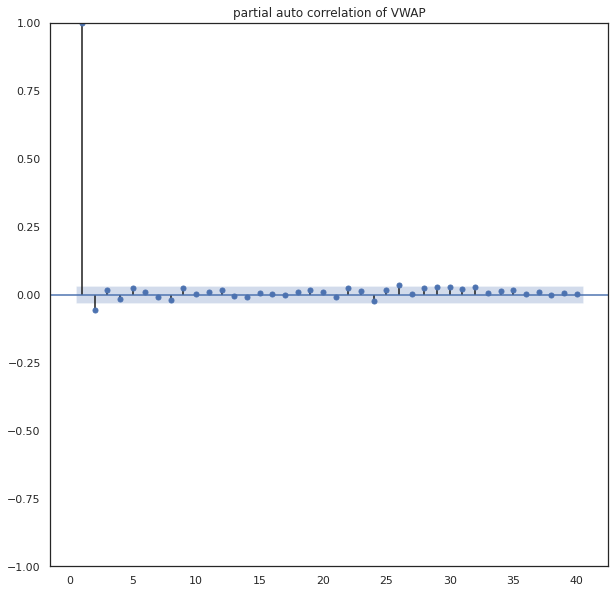
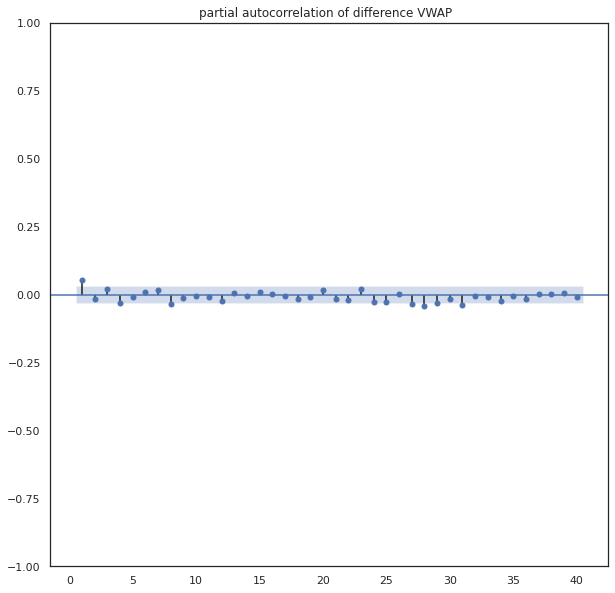
# Feature Engineering

Adding lag values of High, Low, Volume, Turnover, will use three sets of lagged values, one previous day, one looking back 7 days and another looking back 30 days as a proxy for last week and last month metrics.

df.head()

df=df.reset_index()

lag_features = [“High”, “Low”, “Volume”, “Turnover”,”Close”]

window1 = 3

window2 = 7

window3 = 30

df_rolled_3d = df[lag_features].rolling(window=window1, min_periods=0)

df_rolled_7d = df[lag_features].rolling(window=window2, min_periods=0)

df_rolled_30d = df[lag_features].rolling(window=window3, min_periods=0)

df_mean_3d = df_rolled_3d.mean().shift(1).reset_index().astype(np.float32)

df_mean_7d = df_rolled_7d.mean().shift(1).reset_index().astype(np.float32)

df_mean_30d = df_rolled_30d.mean().shift(1).reset_index().astype(np.float32)

df_std_3d = df_rolled_3d.std().shift(1).reset_index().astype(np.float32)

df_std_7d = df_rolled_7d.std().shift(1).reset_index().astype(np.float32)

df_std_30d = df_rolled_30d.std().shift(1).reset_index().astype(np.float32)

for feature in lag_features:

df[f”{feature}_mean_lag{window1}”] = df_mean_3d[feature]

df[f”{feature}_mean_lag{window2}”] = df_mean_7d[feature]

df[f”{feature}_mean_lag{window3}”] = df_mean_30d[feature]

df[f”{feature}_std_lag{window1}”] = df_std_3d[feature]

df[f”{feature}_std_lag{window2}”] = df_std_7d[feature]

df[f”{feature}_std_lag{window3}”] = df_std_30d[feature]

df.fillna(df.mean(), inplace=True)

df.set_index(“Date”, drop=False, inplace=True)

df.Date = pd.to_datetime(df.Date, format=”%Y-%m-%d”)

df[“month”] = df.Date.dt.month

df[“week”] = df.Date.dt.week

df[“day”] = df.Date.dt.day

df[“day_of_week”] = df.Date.dt.dayofweek

df.head()

df_train = df[df.Date < “2019”]

df_valid = df[df.Date >= “2019”]

exogenous_features = [“High_mean_lag3”, “High_std_lag3”, “Low_mean_lag3”, “Low_std_lag3”,

“Volume_mean_lag3”, “Volume_std_lag3”, “Turnover_mean_lag3”,

“Turnover_std_lag3″,”High_mean_lag7”, “High_std_lag7”, “Low_mean_lag7”, “Low_std_lag7”,

“Volume_mean_lag7”, “Volume_std_lag7”, “Turnover_mean_lag7”,

“Turnover_std_lag7″,”High_mean_lag30”, “High_std_lag30”, “Low_mean_lag30”, “Low_std_lag30”,

“Volume_mean_lag30”, “Volume_std_lag30”, “Turnover_mean_lag30”,

“Close_mean_lag3”, “Close_mean_lag7″,”Close_mean_lag30″,”Close_std_lag3″,”Close_std_lag7″,”Close_std_lag30”,

“Turnover_std_lag30″,”month”,”week”,”day”,”day_of_week”]

#Auto ARIMA model

model = auto_arima(df_train.VWAP, exogenous=df_train[exogenous_features], trace=True, error_action=”ignore”, suppress_warnings=True)

model.fit(df_train.VWAP, exogenous=df_train[exogenous_features])

forecast = model.predict(n_periods=len(df_valid), exogenous=df_valid[exogenous_features])

df_valid[“Forecast_ARIMAX”] = forecast

# Model Summary

model.summary()

# Plot VWAP vs Forecast ARIMAX

df_valid[[“VWAP”, “Forecast_ARIMAX”]].plot(figsize=(14, 7))

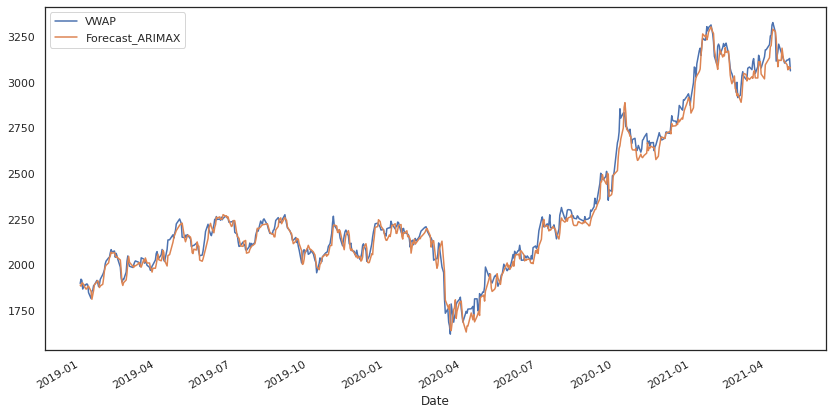
#Analyzing residuals

residuals=df_valid.VWAP-df_valid.Forecast_ARIMAX

dicky_fuller_test((residuals))

#Plot residuals

residuals.plot()

# Model Evaluation

print(“RMSE of Auto ARIMAX:”, np.sqrt(mean_squared_error(df_valid.VWAP, df_valid.Forecast_ARIMAX)))

print(“\nMAE of Auto ARIMAX:”, mean_absolute_error(df_valid.VWAP, df_valid.Forecast_ARIMAX))